Huffman-Encoder using Java

Huffman Coding, named after it's inventor David A. Huffman in 1952, is a means to encrypt texts in order to minimize the amount of data required to transmit the text lossfree.

Each letter present in the text is encoded with a uniquely identifiable series of bits. The length of the bit series is chosen so, that the letters appearing more frequently get encoded by less bits than the letters appearing few times only.

In order to generate these codes, both when doing the encoding manually as well as programmaticaly, a "Huffman Tree" is constructed. For that one starts by counting how often each character is used in the string and then sorting the letters by their count. When doing it graphically, the letters are usually arranged horizontally. The values of the two rarest letters are then summed up and written into a new "bubble" above these letters, containing the aforementioned sum. Next again the lowest possible sum needs to be found, taking the newly generated bubble into consideration, but no longer the letters it was made from. This process is continued until only one "root" bubble remains.

A typical example is the word "Mississippi", as most letters are repeated multiple times and thus the compression rate is especially significant. Its Huffman Tree looks like this:

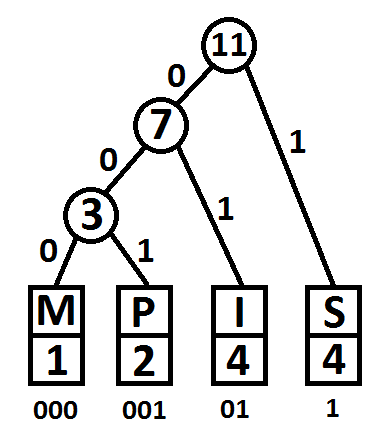
After the tree structure is built, the connections between the bubbles resp. letters are labelled with 0 and 1, so that each bubble has two lower bubbles attached to it, one over a connection labelled "1" and the other labelled "0". It does not matter whether the 0 is placed on the left or right branch as the codes would just be inverted, and a 0-bit takes as much space to store as a 1-bit.

The codes for each letter are now easily generated by following the lines from the root node at the top to the letters and while doing so, concatenating all branch labels.

The Huffman Code for the entire string is simply generated by concatenating the codes for each letter in the order of appearance in the original string. Thus we get for "Mississippi", encoded with this Huffman Tree:

In this special example, the size of the data is reduced from 88 bits to a mere 21 bits. One has to consider though that the key, that is which code represents which letter, also has to be sent, and thus using the Huffman encoding for very short texts is not very effective.

Beside the main class, which I will call "HuffmanEncoder", I use two additional classes:

Class Bubble:

An object of class Bubble represents a single node of a Huffman Tree. The leaves of the tree, containing the letters, are also represented by a Bubble.

The class has the following fields:

bubble0 and bubble1 are references to the two other Bubbles below the Bubble in question. For leaves ("letter-Bubbles") these two are null. The letter field contains the character contained in the Bubble, if it contains one, else this is null. Lastly the value field always contains the count, respectively the sum of the counts of the letters in or below the Bubble.

The class Bubble has two constructors, one for creating a Bubble containing a letter, there the parameters are the letter and its count. The second constructor is for creating a Bubble higher up in the tree. As arguments it takes two other Bubble objects and stores them as its bubble0 and bubble1 fields. The value is set to the sum of the values of the two other Bubbles.

Class HuffmanTree

A HuffmanTree Object represents an entire tree structure. Similar to a Linked List it contains the root element from where the tree can be read over the refernces stored in each node (with the difference that each node has two following elements and not just one). Additionally it contains a HashMap codes to store the codes for each letter once they're generated.

Furthermore it contains two class methods which will be explained in more detail further down: buildCodes, a method which reads the trees and reads and stores each letter's code, and method encode, which encodes a string using the codes gained.

The only constructor takes the root Bubble as parameter. Beside setting that, it initilialises the codes HashMap and then calls the buildCodes function.

The first thing to accomplish in the main method is to create the leaf-Bubbles, i.e. the ones containing the letters along with how often they appear in the input string. The counting does not require splitting the string into a character array as one may consider, a more elegant solution is using Java's string.replaceAll function. The idea is to take the first letter of the string, and remove all occurrences of this letter from the string. The count for this letter is gained by simply subtracting the length of the previous string with the new length. This can be continued until all letters have been removed. To not have to store the gained data somewhere else, the Bubbles are also created within this iteration process:

The algorithm used to build tree is very similar to the process described above. Only that now the tree is not displayed as a graphic but only through Objects and the relations between them.

The, in my opinion most straightforward way to build the tree looks somewhat like this:

- Sort the list with all bubbles in it (created in the process of counting and storing the letters), in ascending order.

- Create a new Bubble linking to the two first elements of that list, and add their sum as the new Bubble's value.

- Insert the new Bubble into the list.

- Remove the two Bubbles used before from the list.

- Repeat until the list has only one Bubble left.

In actual code this might look like this:

What is very straightforward when doing the encoding manually, but does require a little more thought when coding it in an elegant way is how to read the tree, and thus gain the codes for each letter.

What the code needs to do is start reading from the top and then add a "0" or a "1" to the work-in-progress code, depending on which branch it took. This has to be continued until a Bubble is reached which contains a letter.

However if this would be done for every letter in a somewhat separate "session" in which the entire tree is traversed and only one letter code is gained is neither elegant nor very optimised regarding requried operations.

The best way to go is most likely using recursion. The aforementioned method buildCodes is that recursive method. It is initiated by the HuffmanTree constructor who passes the root Bubble (the topmost one) and an empty string to the method. The method now checks whether the Bubble contains a letter or not. If yes, it adds the letter and it's code to the codes HashMap. If not however, the method calls itself again twice, once passing the Bubble on the "0" branch from the current Bubble and once the Bubble on the "1". Along with them it passes the so far assembled code plus either a "1" or "0", depending on the branch.

As mentioned, this function is a class method of the HuffmanTree class. When calling the constructor you need to pass the root Bubble, which is simply the last Bubble remaining in the ArrayList from the last step.

The recursive function may look like this:

After that, putting together the encoded text is no great feat anymore. All that needs doing is browsing the codes HashMap letter by letter and receiving the respective code. Concatenating these yields the encoded message.